import torch
from torch.autograd import grad
import numpy as np
import matplotlib.pyplot as plt
import math
from tqdm import tqdm
class PINNStaticModel:
def __init__(self, input_dim, hidden_dim, output_dim):
"""Initialize the model and loss history."""
self.model = torch.nn.Sequential(
torch.nn.Linear(input_dim, hidden_dim),
torch.nn.Tanh(),
torch.nn.Linear(hidden_dim, output_dim)
)
self.loss_history = {'total': [], 'boundary': [], 'differential': []}
def get_derivative(self, y, x):
"""Compute the derivative of y with respect to x."""
dydx = grad(y, x, torch.ones(x.size()[0], 1),
create_graph=True,
retain_graph=True)[0]
return dydx
def compute_pinn_residual(self, x, EA, p):
"""Compute the residual of the governing differential equation."""
u = self.model(x)
u_x = self.get_derivative(u, x)
EAu_xx = self.get_derivative(EA(x) * u_x, x)
f = EAu_xx + p(x)
return f
def compute_loss(self, x, EA, p):
"""
Compute boundary and differential equation losses.
- Boundary condition loss at x = 0 and x = 1.
- Differential equation loss as the mean squared error of the residual.
"""
# Boundary condition loss
u0_pred = self.model(torch.tensor([[0.0]]))
u1_pred = self.model(torch.tensor([[1.0]]))
MSE_b = (u0_pred - 0)**2 + (u1_pred - 0)**2
# Differential equation loss
f_pred = self.compute_pinn_residual(x, EA, p)
MSE_pde = torch.mean(f_pred**2)
return MSE_b, MSE_pde
def train(self, x, EA, p, epochs=50, lr=0.1):
"""
Train the model with LBFGS optimizer.
Track the progress using tqdm.
"""
optimizer = torch.optim.LBFGS(self.model.parameters(),
lr=lr,
max_iter=20,
max_eval=25,
tolerance_grad=1e-7,
tolerance_change=1e-9,
history_size=50)
pbar = tqdm(total=epochs, desc="Training", position=0, leave=True)
def closure():
optimizer.zero_grad()
MSE_b, MSE_pde = self.compute_loss(x, EA, p)
loss = MSE_b + MSE_pde
loss.backward()
# Update loss history
self.loss_history['total'].append(loss.item())
self.loss_history['boundary'].append(MSE_b.item())
self.loss_history['differential'].append(MSE_pde.item())
# Update progress bar description with current losses
pbar.set_description(f"Loss: {loss.item():.2e}")
return loss
for _ in range(epochs):
optimizer.step(closure)
pbar.update(1)
pbar.close()
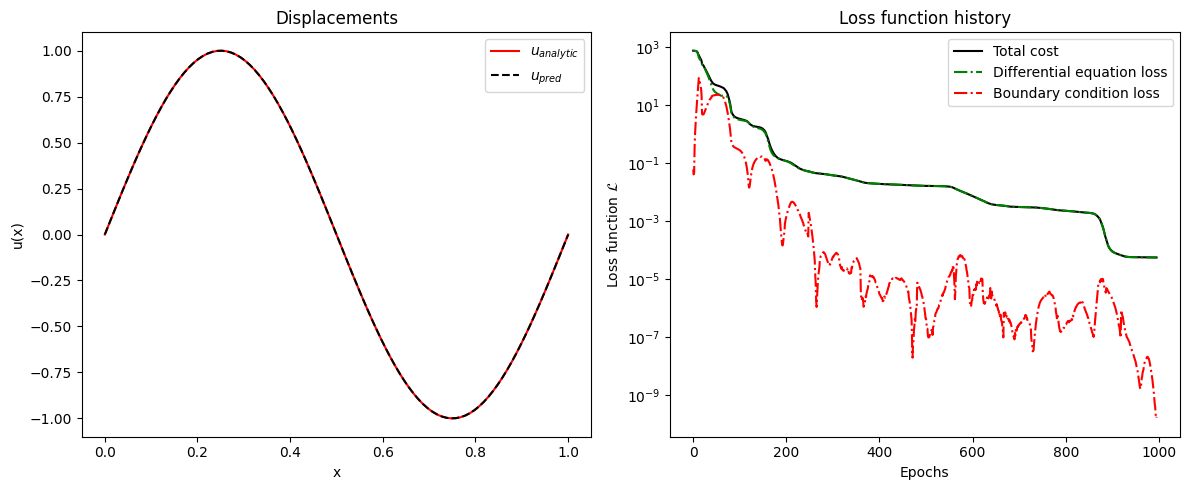
def plot_results(self, x):
"""Plot the model predictions and training loss history."""
plt.figure(figsize=(12, 5))
# Plot 1: Displacements
plt.subplot(1, 2, 1)
x_np = x.detach().numpy()
u_analytic = np.sin(2 * np.pi * x_np)
u_pred = self.model(x).detach().numpy()
plt.plot(x_np, u_analytic, 'r-', label='$u_{analytic}$')
plt.plot(x_np, u_pred, 'k--', label='$u_{pred}$')
plt.xlabel('x')
plt.ylabel('u(x)')
plt.title('Displacements')
plt.legend()
plt.grid(False)
# Plot 2: Cost function history
plt.subplot(1, 2, 2)
epochs = range(len(self.loss_history['total']))
plt.semilogy(epochs, self.loss_history['total'], 'k-', label='Total cost')
plt.semilogy(epochs, self.loss_history['differential'], 'g-.', label='Differential equation loss')
plt.semilogy(epochs, self.loss_history['boundary'], 'r-.', label='Boundary condition loss')
plt.xlabel('Epochs')
plt.ylabel('Loss function $\mathcal{L}$')
plt.title('Loss function history')
plt.legend()
plt.grid(False)
plt.tight_layout()
plt.show()